< Kembali

Notasi O Besar atau Big-O Notation

✏️ Edit catatan ini.

Ketika kita memikirkan apakah barisan kode yang kita ciptakan sudah cukup "cepat" atau efisien dalam memecahkan masalah yang ingin kita pecahkan, maka kita butuh sebuah metodologi untuk menghitungnya. Salah satu alat bantu yang bisa kita gunakan adalah notasi O besar atau Big-O Notation.

Ini juga berarti kita ingin menghitung kompleksitas dari sebuah kode. Ada dua dimensi dalam menghitung kompleksitas kode. Pertama adalah kompleksitas ruang atau space complexity yang berkaitan dengan berapa banyak ruang yang digunakan seperti memori ataupun harddisk komputer. Kedua adalah kompleksitas waktu atau time complexity yang berkaitan berapa lama baris kode dijalankan.

Kenapa dibutuhkan sebuah metode untuk menghitung efisiensi kode? Karena kita tidak bisa hanya mengatakan bahwa kumpulan kode ini dapat dijalankan selama lima detik. Padahal sangat banyak faktor penentu lainnya seperti jumlah datanya, koneksi, latensi, jumlah memori, kecepatan prosesor dan masih banyak yang lainnya.

Karena itu kita butuh alat ukur untuk menghitung efisiensi kode secara relatif seperti notasi O besar ini.

Sekilas Tentang Notasi O Besar

Notasi O besar atau yang lazim disebut dengan Big-O Notation adalah sebuah cara atau metode untuk melakukan analisa terhadap sebuah algoritma pemrograman terhadap waktu eksekusi. Tentang seberapa efisien dan kompleksitas barisan kode dalam dimensi waktu.

Di dalam sebuah program komputer pada umumnya, kita sudah lazim dengan istilah masukan-proses-keluaran.

Notasi O besar merupakan skenario terburuk dari sebuah algoritma, dan biasanya terdapat notasi n yang merepresentasikan jumlah masukan. Berikut adalah diagram notasi O besar dengan masukan yang dimulai dari 0 hingga tak terhingga.

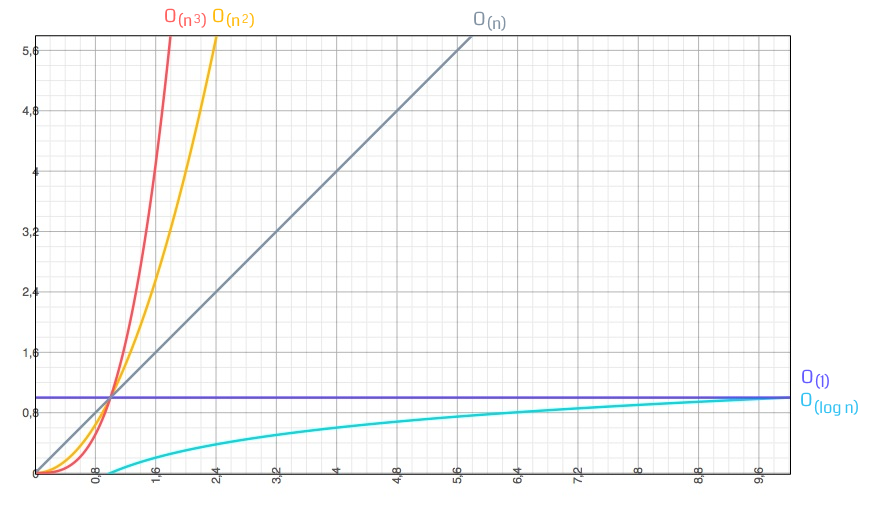
Dari diagram diatas dapat kita lihat beberapa notasi yang kerap muncul, yaitu: O₍₁₎, O_{(log n)}, O_(n), O_(n²) atau O_(nⁿ). Untuk membahasnya, mari kita berandai-andai membangun sebuah aplikasi travel. Dan kita diminta untuk membuat fitur baru yang menampilkan daftar kisaran harga dari hotel-hotel yang berada di area tertentu.

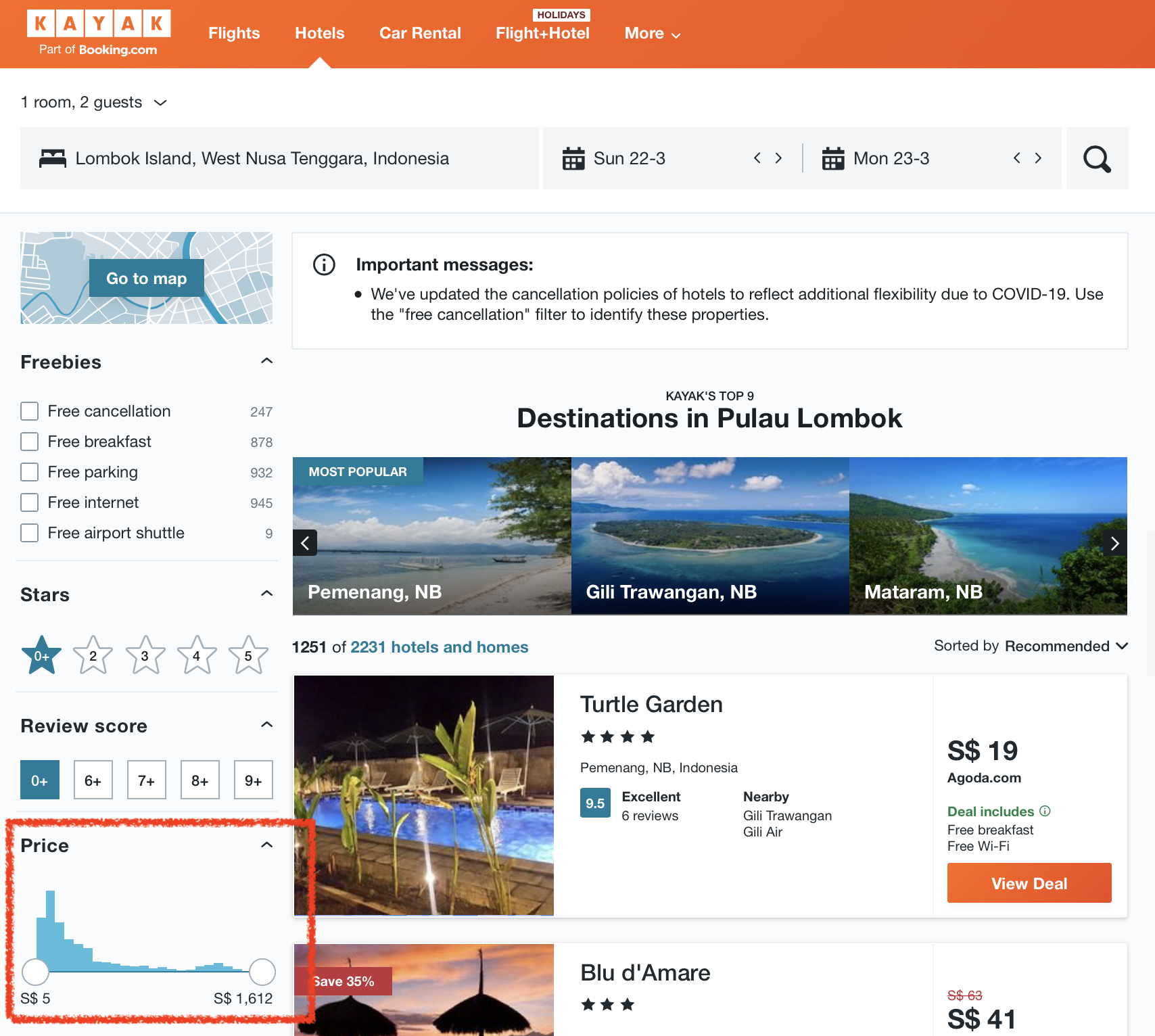
Untuk membuat fitur tersebut, sederhananya kita mencari harga terendah (min) dan harga tertinggi (max) dari daftar hotel. Tentunya semakin banyak datanya, akan semakin lama pula proses untuk mencari harga terendah dan tertinggi.

Dan berikut versi sederhana dari representasi data yang akan kita gunakan. Kita akan menggunakan JavaScript sebagai contoh. Dapat juga diaplikasikan ke bahasa pemrograman lain.

const hotels = [
{ price: 180, brand: "Hotel Tugu Lombok" },
{ price: 78, brand: "Sheraton Senggigi Beach Resort" },
...
...
{ price: 317, brand: "The Oberio" }
]

Pengulangan di Dalam Pengulangan: O_(N²)

Sekarang, bagaimana caranya mencari harga terendah dan tertinggi? Cara yang paling naif adalah dengan membandingkan harga satu-per-satu. Berikut potongan kode sebagai ilustrasi.

for (let i = 0; i < hotels.length; i++) {
  for (let j = 0; j < hotels.length; j++) {
    // kode untuk membandingkan satu harga dengan harga lainnya...
  }
}

Mari kita simulasikan ketika jumlah data semakin banyak.

n	3	5	10	100
Jumlah Operasi	9	25	100	10000

Lihat tabel diatas, antara 3 dan 5 cukup dekat perbedaannya hanya dua. Namun jumlah operasi yang dijalankan sangat signifikan bedanya. Semakin banyak datanya semakin signifikan jumlah operasi yang dijalankan.

Dengan kata lain kita membutuhkan n² dan untuk mencari harga terendah (min) dan harga tertinggi (max). Itulah sebabnya kita menyebutnya dengan notasi O_(n²). Algoritma seperti ini sangatlah lambat dan tidak optimal.

Pengulangan Dari Sebuah Set: O_(N)

Jika solusi pertama tidak optimal, adakah solusi lain? Tentu. Misalnya kita bisa mencari apakah harga adalah yang terendah atau tertinggi dalam satu kali pengulangan saja seperti ilustrasi kode berikut.

for (let i = 0; i < hotels.length; i++) {
  // cari harga paling kecil...
  // cari harga paling besar...
}

Ketika kita membutuhkan proses "pengulangan untuk setiap item", merupakan notasi O_(N).

Hanya Satu Operasi: O₍₁₎

Jika dengan asumsi bahwa data hotels sudah diurutkan berdasarkan harga terendah ke harga tertinggi, maka pencarian harga terendah dan tertinggi menjadi semakin efisien.

const hotels = [
  { price: 78, brand: "Sheraton Senggigi Beach Resort" },
  { price: 180, brand: "Hotel Tugu Lombok" },
  ...
  ...
  { price: 317, brand: "The Oberio" }
]

Untuk mendapatkan harga terendah, kita tinggal memanggil hotels[0].price. Sementara untuk harga tertinggi kita bisa menggunakan hotels[hotels.length-1].price. Selain lebih mudah, eksekusi baris kode juga menjadi lebih cepat dan efisien.

Ketika kode menjalankan sebuah operasi, misalkan: baris kode untuk mencari item barang teratas atau mendapatkan nilai sebuah array dengan indeks ke-5. Operasi seperti ini kita bisa sebut sebagai notasi O₍₁₎.

Tidak masalah sebanyak apapun isi dari sebuah array atau sebanyak apapun jumlah baris di basis data, untuk mengambil nilai array dengan mengakses indeks maka algoritma berjalan secara konstan atau constant time.

Kita sudah melihat beberapa contoh algoritma untuk menampilkan kisaran harga dari yang terendah hingga tertinggi dan hasilnya sebagai berikut.

Notasi O	Istilah Lain	Jumlah Operasi	Algoritma
O(n2)	Quadratic	n2	Komparasi seluruh harga. Pengulangan dalam pengulangan
O(n)	Linear	2n	Mencari harga terendah dan tertinggi. 1 kali pengulangan
O(1)	Constant	2	Asumsi sudah diurut berdasarkan harga, tinggal mencari elemen pertama dan elemen terakhir

Dan secara umum berikut urutan dari notasi O besar diurutkan dari yang tercepat hingga yang terpelan.

<--- Super Cepat --------------------------------------- Super Lambat --------->

Nama	Constant	Logaritmic	Linear	Quadratic	Exponential
Notasi	O(1)	O(log n)	O(n)	O(n2)	O(nn)

Beberapa Contoh Notasi O Besar

Mari kita melihat contoh notasi O besar dari fungsi, ekspresi dan operasi JavaScript yang sederhana.

1. Array.push()

push() merupakan sebuah metode untuk menambahkan item baru kedalam sebuah array. Item yang ditambahkan akan berada diakhir array tersebut. Contoh penggunaan dapat dilihat sebagai berikut.

const animals = ["ants", "goats", "cows"];
animals.push("fish");
console.log(animals); // ['ants', 'goats', 'cows', 'fish']

Apakah notasi yang tepat untuk baris kode animals.push('fish');? Karena metode push() tidak peduli dengan seberapa banyak atau sedikit jumlah item yang ada, artinya operasi yang berjalan tetap sama, maka metode push() ini dapat diwakilkan dengan notasi O₍₁₎ atau konstan.

2. Array.pop()

pop() merupakan sebuah metode yang mengambil item terakhir dari array sehingga jumlah item yang ada di array akan berkurang satu. Berikut contoh penggunaannya.

const plants = ["broccoli", "cauliflower", "cabbage", "tomato"];
plants.pop();
console.log(plants); // ["broccoli", "cauliflower", "cabbage"]

Apakah notasi yang tepat untuk baris kode plants.pop();? Mirip seperti metode push() diatas, metode pop() juga tidak mempermasalahkan jumlah item yang ada, artinya operasi yang berjalan tetap sama, maka metode pop() ini juga dapat diwakilkan dengan notasi O₍₁₎ atau konstan.

3. Array.unshift()

unshift() adalah sebuah metode untuk menambahkan satu atau beberapa item ke bagian awal dari sebuah array. Contoh penggunaannya sebagai berikut.

const array1 = [1, 2, 3];
array1.unshift(4, 5);
console.log(array1); // [4, 5, 1, 2, 3]

Sekilas operasi unshift() ini terlihat seperti operasi yang konstan seperti push() dan pop() namun jika kita melakukan implementasi ulang metode ini, maka akan terlihat notasi yang sebenarnya. Berikut kira-kira implementasi dari unshift(), implementasi naif tentunya sekedar gambaran.

function unshift(arr, newItem) {
  let newArr = [];
  newArr[0] = newItem;
  for (let i = 1; i < arr.length + 1; i++) {
    newArr[i] = arr[i - 1];
  }
  return newArr;
}

Hal yang menambah kompleksitas adalah ketika kita harus mengubah indeks dari array karena kita akan menempatkan item baru di indeks ke-0. Secara otomatis indeks akan bergeser sebanyak satu langkah. Dan karena itu kita menggunakan pengulangan for hingga menjadikan operasi unshift() dapat diwakilkan oleh notasi linear atau O_(n). Kita harus menyadari apa yang dilakukan oleh sebuah fungsi, operasi ataupun pustaka sehingga kita dapat memprediksi kira-kira seberapa tingkat kompleksitasnya.

Menghitung Total Kompleksitas Kode

Setelah sebelumnya kita sudah menghitung kompleksitas satu baris kode, sekarang kita akan menghitung total keseluruhan untuk beberapa baris kode. Kita akan mulai dari contoh sederhana terlebih dahulu.

for (let i = 0; i < 10; i++) {
  // O(n)
  for (let j = 0; j < 10; j++) {
    // O(n)
    console.log(i); // O(1)
    console.log(j); // O(1)
  }
}

Kompleksitas potongan kode diatas dapat dihitung dengan mengalikan notasi-notasi setiap baris. Karena terdapat pengulangan bersarang, maka operasi yang digunakan adalah perkalian. Artinya hasil dari pengulangan bersarang tersebut adalah: O(n) * O(n) = O_(n²).

Jika perintah yang berada di level yang sama seperti:

console.log(i); // O(1)
console.log(j); // O(1)

Maka operasi yang akan kita lakukan adalah menjumlahkan. Sehingga untuk kedua perintah diatas hasilnya adalah O₍₁₎ + O₍₁₎ = O₍₂₎. Jika digabungkan hasilnya menjadi O_(n²) O₍₂₎. Namun biasanya untuk jenis kode diatas cukup dilambangkan dengan O_(n²) _ O₍₂₎ karena O₍₂₎ tidak signifikan perbedaannya.

Mari kita lihat contoh kode berikutnya.

for (let i = 0; i < 10; i++) {
  // O(n)
  console.log(i);
}

for (let j = 0; j < 10; j++) {
  // O(n)
  console.log(j);
}

Potongan kode deiatas dapat dilambangkan sebagai O_(n) ditambah dengan O_(n) sehingga menjadi O_(2n).

Kesimpulan

Sebagai kesimpulan, notasi O besar atau Big-O Notation merupakan metode untuk menghitung kompleksitas dari potongan kode yang kita buat. Sehingga dapat menumbuhkan kesadaran kita untuk mencari alternatif yang lebih baik sebelum data semakin besar dan berdampak kepada performa aplikasi yang kita buat.

Notasi O besar inipun tidak hanya semata berlaku di bagian kode yang kita tulis, namun di database pun berlaku. Jadi proses pengambilan data di database dengan sintaksis SQL yang dapat dianggap sebagai proses perulangan akan sangat tidak efektif jika di bagian algoritma kode kita kembali menggunakan perulangan. Maka proses tersebut akan menjadi O_(n²) karena akan terdapat perulangan didalam perulangan.

Begitu juga halnya jika kita mengambil data dengan tabel yang sudah diindeks. Secara otomatis notasinya akan berubah dari O_(n) menjadi O_{(log n)}.

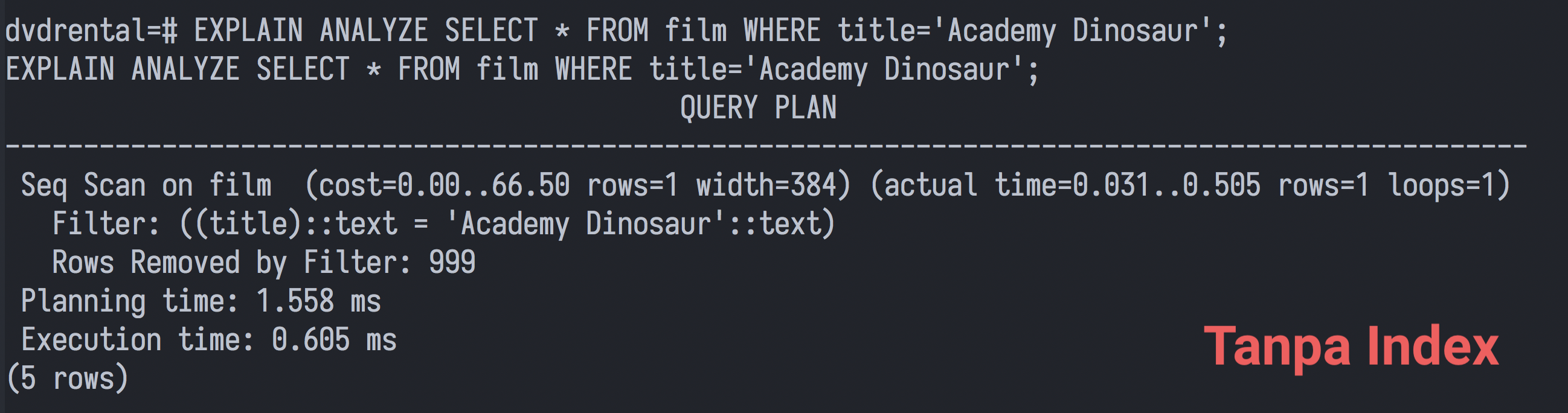
Tanpa menggunakan indeks database melakukan yang disebut dengan "Sequential Scan". Beberapa yang lain menyebutnya dengan istilah "Full Table Scan" yang kurang-lebih melakukan perulangan setiap barisnya dan membandingkan dengan argumen query yang kita tentukan.

Dengan kata lain operasi sequential seperti contoh diatas dapat kita beri notasi O_(n). Seiring bertambahnya jumlah data, efisiensi akan semakin menurun.

Hal termudah untuk mengangkat performa untuk kasus ini adalah dengan menambahkan indeks di tabel terkait dan kita dapat melihat perbedaan yang cukup signifikan terutama ketika data sudah semakin banyak.

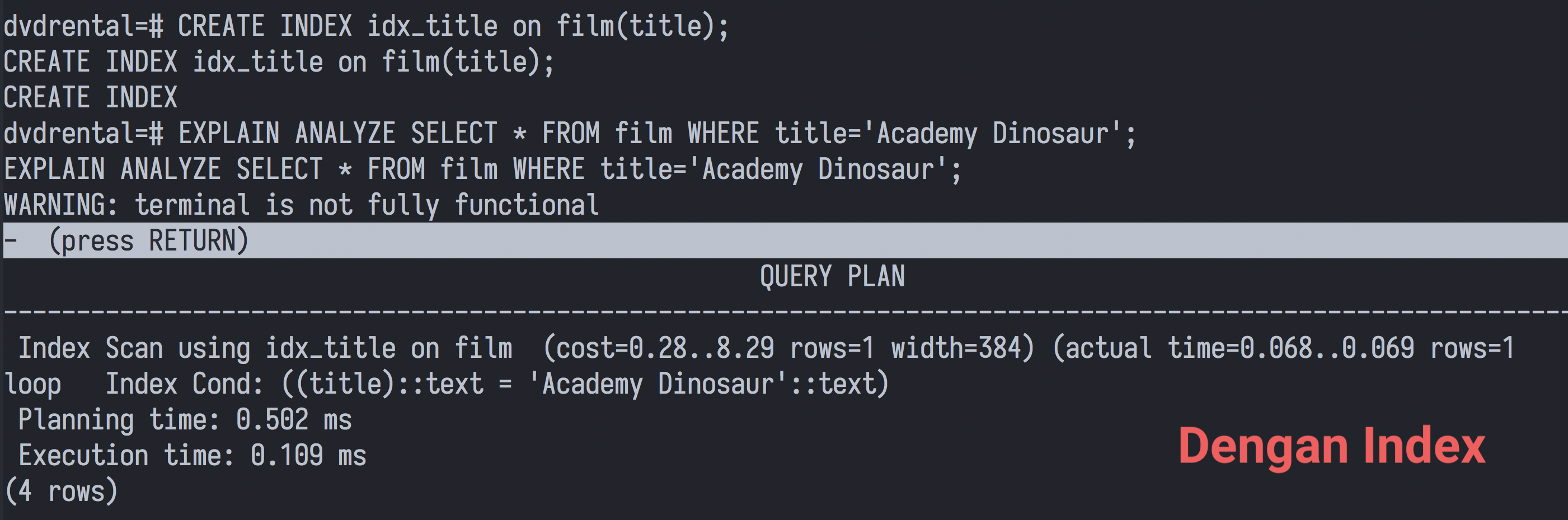
Sehingga operasi diatas berubah notasinya menjadi O_{(log n)}.

Hal yang menarik lainnya, Redis sebuah in-memory database menyertakan notasi kompleksitas waktu di setiap perintah yang ada di dokumentasinya. Contohnya dapat dilihat seperti perintah append, del, lpush, dan masih banyak lagi yang lainnya.

Sebagai penutup, berikut daftar kompleksitas kode dari operasi-operasi yang umum kita jumpai.

Kompleksitas	Operasi
O(1)	Menjalankan sebuah perintah
O(1)	Mendapatkan sebuah item dari array, objek atau variabel
O(log n)	Pengulangan yang berkurang setengahnya setiap iterasi
O(n2)	Pengulangan dalam pengulangan
O(n3)	Pengulangan dalam pengulangan dalam pengulangan

Referensi

• Materi 'Four Semesters of Computer Science in Six Hours'
• Buku 'JavaScript Data Structures and Algorithms, Sammie Bae'
• Video 'FrontendMasters Data Structures and Algorithms in JavaScript, Bianca Gandolfo'

---